译注:作者同意刊载,不过尚未检查翻译准确与否。仓促翻译,可能会有谬误,大家多和原文比对,不正确的地方欢迎邮件我更正。
原文链接:Power Perpetuals
发布于:8.17.2021
作者:Dave White, Dan Robinson, Zubin Koticha, Andrew Leone, Alexis Gauba, Aparna Krishnan
简介
本文介绍了一种新型的衍生品 – 乘方永续合约。
如果 ETH 的价格翻倍,ETH 的 2 次方永续合约翻 4 倍,ETH 的 3 次方永续合约翻 8 倍,ETH 的 5 次方永续合约翻 32 倍。
当然,这种不对称的上涨并不是免费的。那些做多乘方永续合约的人需要定期支付溢价收益,给那些做空的人。
乘方永续合约提供了类似于全球期权的风险敞口,而不需要行权价或到期日,使其有可能将大部分期权市场的流动性,整合到单一的工具中。
从不少方面来讲,乘方永续合约都是 永续期权 合理的下一步。据我们所知,除我们外,研究人员 Wayne Nilsen 和 lllvvuu 也各自独立发现了这种产品。
机制
前提条件
乘方永续合约是 永续期权 论文中介绍的永续衍生品的一个特殊系列。
在本文接下来的内容中,我们将假设读者已经熟悉永续期权和 永续期货 的基本机制。
定义
乘方永续合约是指与某些标的资产价格的乘方挂钩的永续衍生品。在本文中,我们将假设这个标的资产是以太币。
对于任何乘方 p,ETH^p 乘方永续合约都是通过定期(如每天)支付的资金费用来维持的。如果在注资时,乘方永续合约的当前价格是 $MARK,做多乘方永续合约的人必须向做空的人支付 $(MARK-INDEX)=$(MARK-ETH^p)。
在乘方永续合约里,我们把这种资金费用称为 溢价收益 (premium yield)。因为这种费用通常是由多头向空头支付的溢价,以换取类似期权的风险敞口。
例子
考虑 ETH^2 乘方永续合约。
为简单起见,假设 ETH 的交易价格为 $3,而在支付资金时,ETH^2 乘方永续合约的交易价格为 $9.09。那么每份合约多头都将不得不向空头支付 $(MARK-INDEX)=$(MARK-ETH^2)=$(9.09-3^2)=$9.09-$9.00=$0.09。
定价
概述
乘方大于 1 的永续合约具有正的 凸性,这意味着当价格对他们有利时,持有者赚钱更快,而当价格对他们不利时,亏钱则更慢。用期权的话说,我们说它们有正的 伽马值 (gamma)。
就像期权通常以其 内在价值 的溢价交易一样,ETH^p 的乘方永续合约通常以 ETH 价格的 p 次幂的溢价交易。
推导
按照 永续期权论文 中的方法,我们可以先对即将到期的乘方衍生品进行定价,然后这些衍生品的组合进行定价,这个组合刚好相当于所需的永续合约。
下面我们将使用 Black-Scholes 假设来推导我们的价格。这些当然不是最合适的假设,但应该可以作为一个例子来说明做市商如何去给乘方永续合约估值。
在 Black-Scholes 假设下给一个即将到期的乘方衍生品定价要比给期权定价简单得多。有兴趣的读者可以在 StackExchange 这里 找到一个快速推导。其价格为
\[S^pe^{t\frac {p-1}{2}(2r+pv^2)}\]
其中 S 是现货价格,p 是乘方数,t 是到期时间,r 是漂移(drift)或者叫无风险利率,v 是年化波动率。
结合 永续期权论文 附录 B 中的永续期权定价方法,并对所得的几何数列进行求和,我们可以得到每期支付一次资金的乘方永续合约的价格表达式如下(假设数列收敛 – 见下文):
\[S^p\frac {1}{2e^{-f\frac {p-1}{2}(2r+pv^2)}-1}\]
其中 f 是以年为单位的注资期。
这可以解释为指数 S^p 乘以调整系数 \(\frac {1}{2e^{-frac {p-1}{2}(2r+pv^2)}-1}\),该系数考虑了乘方永续合约的嵌入式期权性。需要注意的是,当注资期接近 0 时,这个调整系数接近 1。
溢价收益(我们对融资率的新术语)可以计算为:
\[\text {MARK}-\text {INDEX} = S^P (\frac {1}{2e^{-f\frac {p-1}{2}(2r+pv^2)}-1}-1)\]
收敛性
我们总是可以对股票永续期权进行定价,而与之不同的是,配置不好的乘方永续合约可能会出现价格无法收敛的情况。特别是,我们只有在以下情况下才可以对乘方永续合约进行定价:
\[\frac {e^{f\frac {p-1}{2}(2r+pv^2)}}{2} < 1\]
直观地说,乘方数和波动率越高,长期的临期乘方期货就越有价值;注资期越长,乘方永续合约的价值就越集中于长期的乘方期货。对某些组合来说,同等的投资组合可以变得无限有价值。
这个问题在实践中可以通过选择一个足够小的注资期来轻松避免。
例子
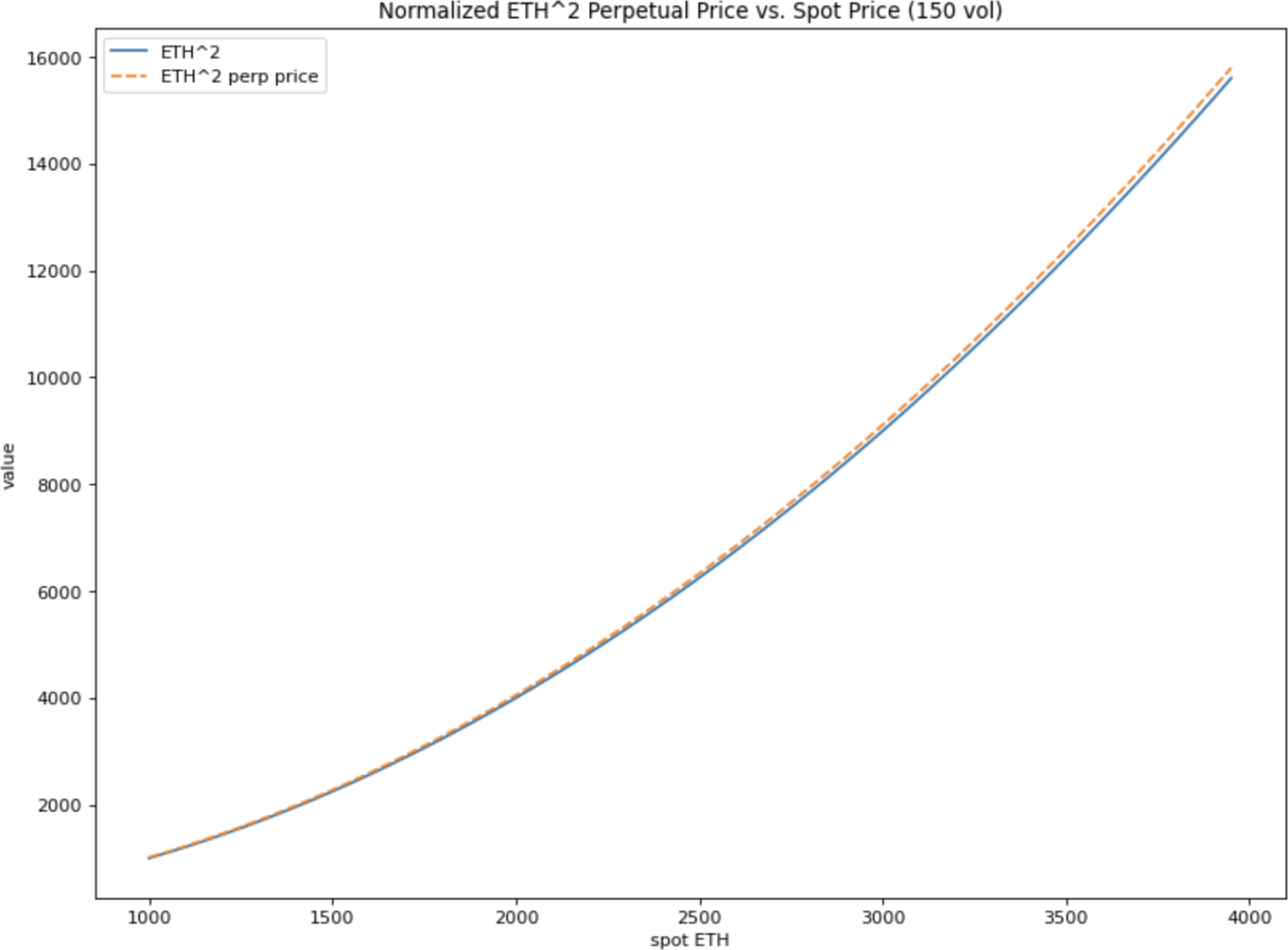
ETH^2 乘方永续合约
见 https://github.com/para-dave/powerperps/blob/master/power_perp_prices.ipynb。
在 Black-Scholes 假设下,ETH^2 乘方永续合约的价格为 \(S^2\frac {1}{2e^{-f(r+v^2)}-1}\)。
在其他条件相同的情况下,当 ETH 价格 4 倍时,它会翻 16 倍。
它有一个很方便的特性,就是有一个恒定的伽马值,即 \(\frac {2}{2e^{-f (r+v^2)}-1}\),这意味着无论 ETH 的价格如何,它都能提供恒定的期权性。
我们亲切地称它为 “squeeth”,是 “ETH 平方” 的简称。
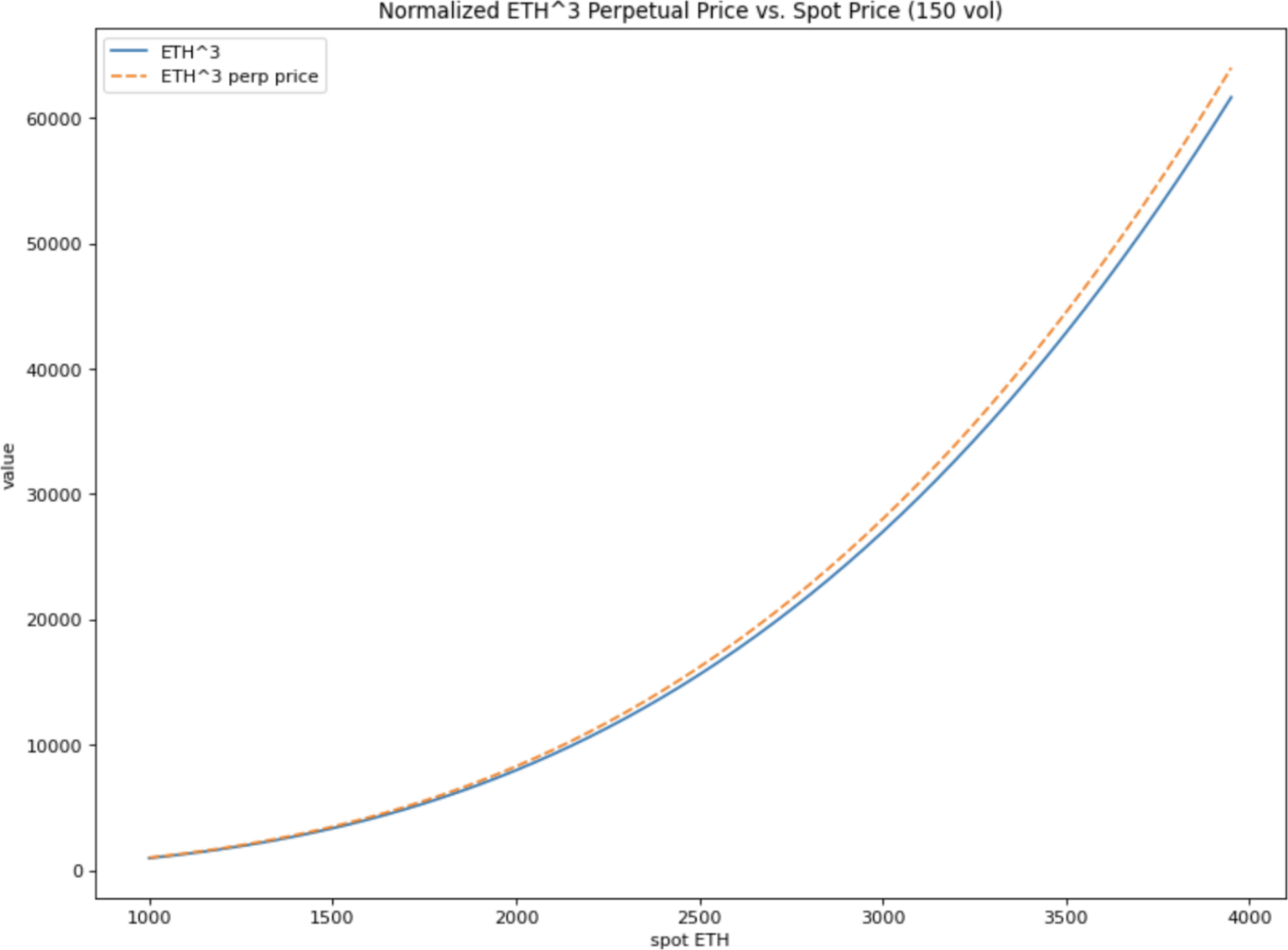
ETH^3 乘方永续合约
见 https://github.com/para-dave/powerperps/blob/master/power_perp_prices.ipynb。
ETH^3 乘方永续合约的价格为 \(S^3\frac {1}{2e^{-f(2r+pv^2)}-1}\)。
在其他条件相同的情况下,ETH 价格翻 4 倍时,它将翻 64 倍。
你可以从图中清楚地看到永续合约的交易价格比其指数 ETH^3 要高,因为它为持有者提供了期权。
Python 定价实现
你可以在 https://github.com/para-dave/powerperps/ 看到乘方永续合约定价的 Python 实现,包括根据经验证明正确性的测试。
总结
乘方永续合约仍处于起步阶段,但我们从 一开始 就对其进行了深入的研究,并仍对其潜力感到非常兴奋。
如果你和我们一样对这种新东西感到好奇,我们很想听听你的想法。你可以发邮件给 dave@paradigm.xyz,或 在 Twitter 上给我发私信,或通过 squeeth@opyn.co,联系 Opyn。
鸣谢:lllvvuu、Wayne Nilsen、Wade Prospere、Grug、Lily Francus、Benn Eifert 博士、Jeff Wang、Mewny